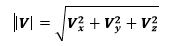Unidad 3: Movimiento en dos o en tres dimensiones

Contenido.

1. Vectores de posición y velocidad. 
2. El vector de aceleración. 
3. Movimiento de proyectiles.
4. Movimiento circular.
5. Ejercicios / Problemas.

Metas de Aprendizaje

Al estudiar esta unidad usted aprenderá: Cómo representar la posición de un cuerpo en dos o en tres dimensiones usando vectores. Cómo determinar el vector velocidad de un cuerpo conociendo su trayectoria. Cómo obtener el vector aceleración de un cuerpo, y por qué un cuerpo puede tener una aceleración aun cuando su rapidez sea constante. Cómo interpretar las componentes de la aceleración de un cuerpo paralela y perpendicular a su trayectoria. Cómo describir la trayectoria curva que sigue un proyectil. Las ideas clave detrás del movimiento en una trayectoria circular, con rapidez constante o con rapidez variable.

1. Vectores de posición y velocidad.

Para describir el movimiento de una partícula en el espacio, primero tenemos que describir su posición. Considere una partícula que está en el punto P en cierto instante.

El vector de posición de la partícula en ese instante es un vector que va del origen del sistema de coordenadas al punto P (figura 38). Las coordenadas cartesianas x, y, z de P son las componentes x, y, z de r.

Usando los vectores unitarios que presentamos en la sección anterior, podemos escribir:

ṝ = xî + yĵ + zk

Figura 38: Vector posición del origen al punto P.

Durante un intervalo de tiempo Δt, la partícula se mueve de P_l, donde su vector de posición es r₁ a P₂, donde su vector de posición es r_2.

El cambio de posición (desplazamiento) durante este intervalo es:

Δr = r_{2 -} r₁

Figura 39: Trayectoria de la partícula.

Definimos la velocidad media durante este intervalo igual que en la unidad 2 para movimiento rectilíneo, como el desplazamiento dividido entre el intervalo de tiempo:

V_med = Δr / Δt

Para definir la velocidad instantánea, es más sencillo calcular el vector de velocidad instantánea empleando componentes.

Durante cualquier desplazamiento los cambios Δx, Δy, Δz en las tres coordenadas de la partícula son las componentes de Δr, por lo tanto, las componentes Vx, Vy y Vz de la velocidad instantánea V son simplemente las derivadas en el tiempo de x, y, z.

Vx = dx / dt                     Vy = dy / dt                   Vz= dz / dt

Los vectores unitarios î, ĵ, k, tienen magnitud y dirección constantes, así que sus derivadas son cero; entonces:

Esto muestra otra vez que las componentes de V son dx/dt, dy/dt, dz/dt.

La magnitud del vector de velocidad instantánea V, esto es, la rapidez, está dada en términos de las componentes Vx, Vy, Vz aplicando el teorema de Pitágoras.

La figura 40, muestra la situación cuando la partícula se mueve en el plano xy.

Aquí, z y Vz son cero, y la rapidez (la magnitud de V) es:

y la dirección de la velocidad instantánea V está dada por el ángulo α de la figura 40.

Tan α = Vy / Vx

Figura 40: Componentes de la velocidad. 

Ejemplo:

1. Se está usando un vehículo robot para explorar la superficie de Marte. El módulo de descenso es el origen de coordenadas; en tanto que la superficie marciana circundante está en el plano xy. El vehículo, que representamos como un punto, tiene coordenadas x e y que varían con el tiempo:

a) Obtenga las coordenadas del vehículo y su distancia con respecto al módulo en t = 2 s.

b) Obtenga los vectores de desplazamiento y velocidad media del vehículo entre t =0 s y t = 2 s.

c) Literal Propuesto. 

Deduzca una expresión general para el vector de velocidad instantánea del vehículo.

Exprese la velocidad instantánea en t = 2 s en forma de componentes y además en términos de magnitud y dirección.

Solución:

a) Coordenadas del vehículo.

x = 2 m – (0,25 m/s²) (2 s)² = 1 m

y = 1 m/s (2 s) + (0,025 m/s³) (2 s)³ = 2,2 m

r² = (1 m)² + (2,2 m)² = 2,4 m

b)Para obtener el desplazamiento y la velocidad media, expresamos el vector de posición r, en función del tiempo t.

En el instante t = 0 s

r_o = (2 m) î + (0 m) ĵ

En el instante t = 2 s

r₂ = (1 m) î + (2,2 m) ĵ

Por lo tanto, el desplazamiento entre t = 0 s hasta t = 2 s

Δr = r₂ - r_o = (1 m) î + (2,2 m) ĵ - (2 m) î + (0 m) ĵ = (-1 m) î + (2,2 m) ĵ

La velocidad media es el desplazamiento dividido por el tiempo transcurrido: 

2. El vector de aceleración.

Consideremos ahora la aceleración de una partícula que se mueve en el espacio. Al igual que en el movimiento rectilíneo, la aceleración describe el cambio en la velocidad de la partícula; en la siguiente figura se muestra el vector aceleración media.

Figura 41: Movimiento de un automóvil.

a_med = ΔV / Δt

La aceleración media es una cantidad vectorial en la misma dirección que el vector ΔV

Definimos la aceleración instantánea a, en el punto P1 como el límite de la aceleración media cuando el punto P2 se acerca a Pl, donde ΔV y Δt se acercan a cero.

El vector de velocidad V, es tangente a la trayectoria de la partícula. No obstante, las figuras muestran que, si la trayectoria es curva, el vector de aceleración instantánea siempre apunta hacia el lado cóncavo de la trayectoria, es decir, hacia el interior de cualquier curva descrita por la partícula.

Cada componente del vector de aceleración es la derivada de la componente correspondiente de la velocidad:

a_x = dVx/dt                     a_y = dVy/dt                        a_z = dVz/dt

La componente x de las ecuaciones, para la aceleración instantánea en una dimensión se puede apreciar en la siguiente figura, muestra un ejemplo del vector aceleración que tiene componentes tanto x como y.

Figura 42: Arquero disparando flecha

Además, como cada componente de velocidad es la derivada de la coordenada correspondiente, expresamos las componentes ax, ay y az del vector aceleración como:

a_x = d²x/dt²                     a_y = d²y/dt²                        a_z = d²z/dt²

3. Movimiento de proyectiles.

Un proyectil es cualquier cuerpo que recibe una velocidad inicial y luego sigue una trayectoria determinada totalmente por los efectos de la aceleración gravitacional y la resistencia del aire. Una pelota bateada, un balón lanzado, un paquete soltado desde un avión y una bala disparada de un rifle son todos proyectiles. El camino que sigue un proyectil es su trayectoria.

Para analizar este tipo de movimiento tan común, partiremos de un modelo idealizado que representa el proyectil como una partícula con aceleración (debida a la gravedad) constante tanto en magnitud como en dirección. Despreciaremos los efectos de la resistencia del aire, así como la curvatura y rotación terrestres.

Como todos los modelos, este tiene limitaciones. La curvatura de la Tierra debe considerarse en el vuelo de misiles de largo alcance; en tanto que la resistencia del aire es de importancia vital para un paracaidista. No obstante, podemos aprender mucho analizando este modelo sencillo.

El movimiento de un proyectil siempre está limitado a un plano vertical determinado por la dirección de la velocidad inicial.

La clave del análisis del movimiento de proyectiles es que podemos tratar por separado

las coordenadas x e y.

Figura 43: Trayectoria de un proyectil.

Las componentes de la velocidad son: 

Figura 44: Componentes de la velocidad de un proyectil.

Usando las ecuaciones de los movimientos anteriormente vistos, podemos simplificar las ecuaciones del movimiento de proyectiles:

Videos: Movimiento de Proyectiles.

4. Movimiento circular.

Cuando una partícula se mueve en una trayectoria curva, la dirección de su velocidad cambia. Como vimos anteriormente, esto implica que la partícula debe tener una componente de aceleración perpendicular a la trayectoria, incluso si la rapidez es constante. En esta sección calcularemos la aceleración para el caso especial importante de movimiento en un círculo.

Figura 45: Automóvil con movimiento circular uniforme.

Movimiento circular uniforme

Cuando una partícula se mueve en un círculo con rapidez constante, tiene un movimiento circular uniforme. Un automóvil que da vuelta a una curva de radio constante con rapidez constante, un satélite en órbita circular y un patinador que describe un circulo con rapidez constante son ejemplos de este movimiento.

Agregamos el subíndice “rad” para recordar que la dirección de la aceleración instantánea

siempre sigue un radio del círculo, hacia su centro.

Como la rapidez es constante, la aceleración siempre es perpendicular a la velocidad instantánea.

a_rad = V² / R

en un tiempo T, la partícula recorre una distancia igual a la circunferencia:

V = 2π R / T

Se puede expresar en términos de su periodo:

a_rad = 4π² R / T²

 

Figura 46: Aceleración y velocidad para una partícula con M.C.U.

Movimiento circular no uniforme

En el movimiento circular no uniforme también hay una componente de aceleración paralela a la velocidad instantánea. Esta es la componente que vimos en la sección anterior, y aquí la llamamos aceleración tangencial para destacar que es tangente al círculo.

Por lo dicho al final de la sección, sabemos que la componente de aceleración tangencial, es igual a la tasa de cambio de la rapidez. Entonces:

a_rad = V² / R                                                         a_tan = d ⎸V ⎸ / dt

Figura 47: Movimiento en un lazo vertical como carro de montaña rusa con rapidez variable. 

Videos: Movimiento circular uniforme y no uniforme.

5. Ejercicios / Problemas.

1. Enlace: Ejemplos resueltos Movimiento de proyectiles
2. Enlace: Problemas resueltos de Proyectiles
3. Enlace: Problemas resueltos proyectiles