Unidad 1: Unidades, Cantidades y Sistemas de referencia

Contenido. 



  1. Estándares y unidades.
  2. Consistencia y conversiones de unidades.
  3. Incertidumbre y cifras significativas.
  4. Estimaciones y órdenes de magnitud.
  5. Magnitudes, Vectores, Sistemas de coordenadas y Suma de vectores.
  6. Producto de vectores.
  7. Ejercicios / Problemas.

Metas de Aprendizaje
Al estudiar esta unidad usted aprenderá:
  • Cuáles son las cantidades fundamentales de la mecánica y cuáles son las unidades que los físicos utilizan para medirlas.
  • Cómo manejar cifras significativas en sus cálculos. 
  • La diferencia entre magnitudes escalares y vectoriales.
  • Cuáles son las componentes de un vector, como sumar y restar vectores gráficamente.
  • Dos formas de multiplicar vectores.


1. Estándares y unidades. 


1.1 Estándares.
Figura 1: Uso de Calibrador Vernier.
La física es una ciencia experimental, que requiere mediciones, cuyos resultados suelen describirse con números. Un número empleado para describir cuantitativamente un fenómeno físico es una cantidad física. Algunas cantidades físicas son tan básicas que sólo podemos definirlas describiendo la forma de medirlas; es decir, con una definición operativa.

Ejemplo: Medir una distancia con una regla, o un lapso de tiempo con un cronómetro.
Ahora, definimos una cantidad física describiendo la forma de calcularla a partir de otras cantidades medibles. Así, podríamos definir la rapidez promedio de un objeto en movimiento, como la distancia recorrida (medida con una regla) entre el tiempo de recorrido (medido con un cronómetro).

Al medir una cantidad, siempre la comparamos con un estándar de referencia. Si decimos que un Porsche Carrera GT tiene una longitud de 4.61 m, queremos decir que es 4.61 veces más largo que una vara de metro, que por definición tiene 1 m de largo.
Dicho estándar define una unidad de la cantidad. El metro es una unidad de distancia; y el segundo, de tiempo. Al describir una cantidad física con un número, siempre debemos especificar la unidad empleada; describir una distancia simplemente como “4.61” no tendría significado. Las mediciones exactas y confiables requieren unidades inmutables que los observadores puedan volver a utilizar en distintos lugares.
Figura 2: Medición del tiempo
(reloj de arena)

Tiempo.

De 1889 a 1967, la unidad de tiempo se definió como cierta fracción del día solar medio (el tiempo promedio entre llegadas sucesivas del Sol al cenit). El estándar actual, es mucho más preciso; se basa en un reloj atómico que usa la diferencia de energía entre los dos estados energéticos más bajos del átomo de cesio. 
Al bombardearse con microondas de cierta frecuencia exacta, el átomo de cesio sufre una transición entre dichos estados. Un segundo (que se abrevia como s) se define como el tiempo que tardan 9,192,631,770 ciclos de esta radiación de microondas.
Longitud
En 1960 se estableció también un estándar atómico para el metro, utilizando la longitud de onda de la luz anaranjada-roja emitida por átomos de kriptón (86Kr) en un tubo de descarga de luz. Usando este estándar de longitud, se comprobó que la rapidez de la luz en el vacío era de 299,792,458 m/s. En noviembre de 1983, el estándar de longitud se modificó otra vez, de manera que la rapidez de la luz en el vacío fuera, por definición, exactamente de 299,792,458 m/s. El metro se define de modo que sea congruente con este número y con la definición anterior del segundo. Así, la nueva definición de metro (que se abrevia m) es la distancia que recorre la luz en el vacío en 1/299,792,458 segundos. Éste es un estándar de longitud mucho más preciso que el basado en una longitud de onda de la luz.

Masa
Figura 3: Estándar de masa (platino-iridio)
El estándar de masa, el kilogramo (que se abrevia kg), se define como la masa de un cilindro de aleación platino-iridio específico que se conserva en la Oficina Internacional de Pesos y Medidas en Sèvres, cerca de París. Un estándar atómico de masa sería más fundamental; sin embargo, en la actualidad no podemos medir masas a escala atómica con tanta exactitud como a escala macroscópica. El gramo (que no es una unidad fundamental) es de 0.001 kilogramos.

1.2 Sistemas de unidades.

1.2.1 Sistema c.g.s.

 Sistema Cegesimal de Unidades, también llamado sistema cgs, es un sistema de unidades basado en el centímetro, el gramo y el segundo. Su nombre es el acrónimo de estas tres unidades. Este sistema se ha reemplazado por el Sistema Internacional de Unidades. Sin embargo, en algunos campos científicos su uso es muy ventajoso en algunos contextos. Así, muchas de las fórmulas del electromagnetismo presentan una forma mas sencilla cuando se las expresa en unidades cgs.

Magnitud
Nombre
Símbolo
Definición
Equivalencia en SI
Longitud
centímetro
cm
0,01 m
Masa
gramo
g
0,001 kg
tiempo
segundo
s
1 s
Aceleración
gal
Gal
cm/s2
0,01 m/s2
Fuerza
dina
dyn
g.cm/s2
10-5 N
Energía
ergio
erg
dyn cm
10-7 J
Potencia
ergio por segundo
erg s-1
10-7 W
Presión
baria
baria
dyn/cm2
0,1 Pa
Viscosidad dinámica
poise
P
g (cm s)-1
0,1 Pa s
Viscosidad cinemática
stokes
St
cm2s-1
10-4 m2s-1
Carga eléctrica
franklin o estatculombio
Fr
dyn½cm
3,336 641×10-10 C
Potencial eléctrico
estatvoltio
statV
erg Fr-1
299,7925 V
Campo eléctrico
estatvoltio por cm
statV cm-1
Flujo magnético
maxwell
Mx
G cm2
10-8 Wb
Densidad de flujo magnético
gauss
Gs, G
Mx cm-2
10-4 T
Intensidad de campo magnético
oersted
Oe
(103/4π) A/m
Intensidad de corriente
estatamperio
statA
3.335 641 × 10-10 A
Resistencia
estatohmio
statΩ
8.987 552 × 1011 Ω
Capacidad eléctrica
estatfaradio o «centímetro»
«cm»
1,113 × 10-12 F
Inductancia
estathenrio
statH
8,988 × 1011 H

1.2.2 Sistema inglés.
El Sistema Inglés de unidades son las unidades no-métricas que se utilizan actualmente en los Estados Unidos y en muchos territorios de habla inglesa (como en el Reino Unido), pero existen discrepancias entre los sistemas de Estados Unidos e Inglaterra. Este sistema se deriva de la evolución de las unidades locales a través de los siglos, y de los intentos de estandarización en Inglaterra.

Hoy en día, estas unidades están siendo lentamente reemplazadas por el Sistema Internacional de Unidades, aunque en Estados Unidos la inercia del antiguo sistema y el alto costo de migración ha impedido en gran medida el cambio.

Longitud
Masa
Volumen
1 milla = 1.609 m
1 libra = 0.454 kg.
1 yarda3 = 0,765 m3
1 yarda = 0.915 m
1 onza = 0.02835 kg.
1 pie3 = 0,02832 m3
1 pie = 12 pulg = 0,3048 m
1 ton. Inglesa = 907 kg.
1 pulg3 = 0,0000164 m3
1 pulgada = 0.0254 m

1 galón = 3,785 L
1 mil = 25,4 μm



1.2.3 Sistema Internacional SI.

 El sistema de unidades empleado por los científicos e ingenieros en todo el mundo se denomina comúnmente “sistema métrico” aunque, desde 1960, su nombre oficial es Sistema Internacional, o SI.

A continuación, se presenta una tabla con las unidades y prefijos del Sistema Internacional (SI) desarrollado por la Conferencia General de Pesos y Medidas.


Unidades básicas del SI
Magnitud
Nombre de la unidad
Símbolo de la unidad
Longitud
Metro
m
Masa
Kilogramo
kg
Tiempo
Segundo
s
Corriente eléctrica
Ampere
a
Temperatura termodinámica
Kelvin
k
Cantidad de sustancia
Mol
mol
Intensidad luminosa
Candela
cd
Unidades derivadas del SI
Área
metro cuadrado
m2
Volumen
metro cúbico
m3
Frecuencia
hertz
Hz
Densidad de masa (densidad)
kilogramo por metro cúbico
Kg/ m3
Rapidez, velocidad
metro por segundo
m/s
Velocidad angular
radián por segundo
rad/s
Aceleración
metro por segundo cuadrado
m/ s2
Aceleración angular
radián por segundo cuadrado
rad/ s2
Fuerza
newton
N
Presión (esfuerzo mecánico)
pascal
Pa
Viscosidad cinemática
metro cuadrado por segundo
m2/s
Viscosidad dinámica
newton-segundo por metro cuadrado
N.s/ m2
Trabajo, energía, cantidad de calor
joule
J
Potencia
watt
W
Cantidad de electricidad
coulomb
C
Diferencia de potencial, fuerza electromotriz
volt
V
Intensidad de campo eléctrico 
volt por metro
V/m
Resistencia eléctrica
ohm
Ω
Capacitancia
farad
F
Flujo magnético
weber
Wb
Inductancia
henry
H
Densidad de flujo magnético
tesla
T
Intensidad de campo magnético
ampere por metro
A/m
Flujo luminoso
lumen
lm
Entropía
Joule por kelvin
J/K
Capacidad de calor específico   
Joule por kilogramo-kelvin
J/ kg.K
Conductividad térmica
Watt por metro-kelvin
W/ m.K


Prefijo
Símbolo
Factor
yotta
Y
1024 (un cuatrillón)
zetta
Z
1021 (mil trillones)
exa
E
1018 (un trillón)
peta
P
1015 (mil billones)
tera
T
1012 (un billón)
giga
G
109 (mil millones)
mega
M
106 (un millón)
miria
ma
104 (diez mil)
kilo
k
103 (mil)
hecto
h
102 (cien)
deca
da
101 (diez)
deci
d
10-1 (un décimo)
centi
c
10-2 (un centésimo)
mili
m
10-3 (un milésimo)
micro
µ
10-6 (un millonésimo)
nano
n
10-9 (un milmillonésimo)
pico
p
10-12 (un billonésimo)
femto
f
10-15 (un milbillonésimo)
atto
a
10-18 (un trillonésimo)
zepto
z
10-21 (un miltrillonésimo)
yocto
y
10-24       (un cuatrillonésimo)




2. Consistencia y conversiones de unidades.


 2.1 Conversión de unidades

 La conversión de unidades, es la transformación del valor numérico de un magnitud física, expresado en una unidad de medida, en otro valor numérico equivalente y expresado en otra unidad de medida de la misma naturaleza. Este proceso suele realizarse con el uso de los factores de conversión y/o tablas de conversión de unidades.
frecuentemente, basta multiplicar por una fracción (factor de una conversión) y el resultado es otra medida equivalente, en la que han cambiado las unidades. Cuando el cambio de unidades implica la transformación de varias unidades, se pueden utilizar varios factores de conversión uno tras otro, de forma que el resultado final será la medida equivalente en las unidades que buscamos.
Tabla de conversión de unidades
Magnitud
Unidad
Conversiones
longitud
metro (m)
1 m = 100 cm = 1000 mm
1 m = 3,281 pies (ft)
1 ft = 12 pulgadas (in)
1 in = 0,0254 m
volumen

1 m3 = 1000 litros
1 m3 = 35,32 ft3 = 264,17 galones
masa
kilogramo (Kg)
1 kg = 1000 g = 0,001 toneladas
1 kg = 2,205 lb
1 lb = 16 onzas
fuerza
newton (N)
1 N = 1 kg-m/s2 = 105 dinas (g-cm/s2)
1 N = 0,1020 kgf = 0,2248 lbf
1 kgf = 2,205 lbf
energía
joule (J)
1 J = 1 N-m = 1 W-s = 107 erg (dina-cm)
1 J = 0,7376 lbf-ft = 2,78 *10-7 KWH
1 J = 0,2389 calorías = 9,48 *10-4 BTU
1 BTU = 252 calorías
potencia
watt (W)
1 W = 1 J/s
1 W = 1,34*10-3 caballos (hp)
1 hp = 76,1 kgf-m/s
presión
pascal (Pa)
1 Pa = 1 N/ m2 = 10 dina/cm2 = 10-5 bar
1 Pa = 0,1020 kgf/cm2 = 1,45*10-4 psi
1 Pa = 9,9*10-6 atm
1 atm = 101,325 KPa
1 atm = 14,7 psi = 1,030 kgf/cm2
1 Pa = 760 torr = 760 mmHg
densidad

1 Kg/m3 = 0,001 g/cm3
1 Kg/m3 = 0,06243 lb/ft3
viscosidad dinámica
(Pa-s)
1 Pa-s = 1 kg/m-s = 10 poise
1 poise = 1 g/cm-s = 100 cp
1 mPa-s = 1 cp
1 Pa-s = 0,1020 kgf-s/m2
1 Pa-s = 0,02089 lbf-s/ ft2
viscosidad cinemática
(stoke)
1 stoke = 1 cm2/s = 100 centistoke
1 stoke = 10-4 m2/s
velocidad angular

1 rad/s = 60/2π RPM
diferencia de temperaturas

1 ºC = 1 ºK = 1,8 ºF = 1,8 ºR
escalas de temperatura

T (ºF) = 1,8 T (ºC) + 32
T (K) = T (ºC) + 273,15
T (ºR) = T (ºF) + 459,6
constante universal de los gases

R = 1,987 BTU / lbmol - ºR
R = 82,06 atm- cm3 / mol-K
R = 8,314 N/m2 - m3 / mol-K
aceleración de gravedad

g = 9,8 m/s2
g = 32,17 ft/s2




2.2 Factores de conversión.

 Es un método de conversión, donde el numerador y el denominador son cantidades iguales expresadas en unidades de medida distintas y se basa en multiplicar por una o varias fracciones de tal manera, que cada fracción equivale a la unidad.

Ejemplo 1:
El diamante tallado más grande del mundo es la Primera Estrella de África (montada en el cetro real británico y guardado en la Torre de Londres). Su volumen es de 1,84 pulgadas cúbicas. ¿Cuál será su volumen en centímetros cúbicos? ¿Y en metros cúbicos?


Ejemplo 2:
El récord mundial en 100 metros lisos lo consiguió Usain Bolt en el año 2009 con 9,58 segundos durante el campeonato mundial de Berlín.  Exprese esta rapidez en Km/h.



3. Incertidumbre y cifras significativas 

Figura 4: Incertidumbre de medición. 

3.1 Incertidumbre

El Vocabulario Internacional de Meteorología (VIM) define la incertidumbre de medida como un parámetro, asociado al resultado de una medición, que caracteriza la dispersión de los valores que razonablemente podrían ser atribuidos al mesurando.



 Todas las mediciones tienen asociada una incertidumbre que puede deberse a los siguientes factores:

v  Naturaleza de la magnitud que se mide.
v  Instrumento de medición.
v  El observador.
v  Condiciones externas.


Cada uno de estos factores constituye por separado una fuente de incertidumbre y contribuye en mayor o menor grado a la incertidumbre total de la medida. La tarea de detectar y evaluar las incertidumbres no es simple e implica conocer diversos aspectos de la medición.

En principio, es posible clasificar las fuentes de incertidumbres en dos conjuntos bien diferenciados, las que se deben a:
  • Errores accidentales o aleatorios, que aparecen cuando mediciones repetidas de la misma variable dan valores diferentes, con igual probabilidad de estar por arriba o por debajo del valor real. Cuando la dispersión de las medidas es pequeña se dice que la medida es precisa.
  • Errores sistemáticos, que son una desviación constante de todas las medidas ya sea siempre hacia arriba o siempre hacia abajo del valor real y son producidos, por ejemplo, por la falta de calibración del instrumento de medición.

En esta figura podemos diferenciar los errores sistemáticos y errores aleatorios. Los centros de los círculos indican la posición del valor que se quiere medir y las cruces indican los valores de varias mediciones.

La dispersión de los puntos se asocia a la precisión y su centro efectivo está asociado a la exactitud.

 a) Precisa pero inexacta.
b) Más exacta y más precisa.
c) Menos precisa y menos exacta.
d) Exacta pero menos precisa. 


Figura 5: Ilustración esquemática de los conceptos de precisión y exactitud 


3.2  Cifras significativas

   Las cifras significativas representan el uso de una o mas escalas de incertidumbre en determinadas aproximaciones. También, cuando queremos expresar una medida con un determinado número de cifras significativas deben seguirse las siguientes reglas: 


Regla
Ejemplo
Son significativos todos los dígitos distintos de cero.
8321 tiene cuatro cifras significativas.
Los ceros situados entre dos cifras significativas son significativos.
104 tiene tres cifras significativas.
Los ceros a la izquierda de la primera cifra significativa no lo son.
0,005 tiene una cifra significativa.
Cuando la cifra a redondear, le sigue 5 se considera si es par o impar.
Si es impar se incremente en 1 dígito y si es par se deja igual.
12,35 por lo tanto, se incrementa quedando 12,4.
12,25 por ser par se mantiene su valor y queda 12,2.
Para números mayores que 1, los ceros a la derecha de la coma son significativos.
8,00 tiene tres cifras significativas.
Para números sin coma decimal, los ceros posteriores a la última cifra distinta de cero pueden o no considerarse significativos. Así, para el número 70 podríamos considerar una o dos cifras significativas. Esta ambigüedad se evita utilizando la notación científica.
7·102 tiene una cifra significativa.
7,0·102 tiene dos cifras significativas.




4. Estimaciones y órdenes de magnitud 


Figura 6: Diferentes órdenes de magnitud de volumen.

 Destacamos la importancia de conocer la precisión y exactitud de los números que representan cantidades físicas. Pero, a menudo incluso una estimación burda de una cantidad puede darnos información útil. Normalmente, sabemos cómo calcular cierta cantidad, pero tenemos que estimar los datos necesarios para el cálculo. De vez en cuando, el cálculo suele ser demasiado complicado para efectuarse con exactitud, así que lo aproximamos. En ambos casos, nuestro resultado es una estimación, pero nos servirá aun si tiene un factor de incertidumbre de dos, diez o mas. Estos cálculos, se denominan estimaciones de orden de magnitud. El gran físico italo-estadounidense Enrico Fermi (1901-1954) los llamaba "cálculos del reverso de un sobre". 



Ejemplo: Estimación de orden de magnitud
Supongamos que una persona huye a otro país con mil millones de dólares en oro en la maleta. ¿Es posible esto? ¿Cabría tanto oro en una maleta?


Solución.
El oro se vende a unos 1200 dólares la onza; aunque el precio varía entre 1100 y 1300 dólares. Una onza equivale a unos 28 g. por lo tanto, podemos suponer que 40 dólares es aproximadamente 1 g. Así que mil millones (109) de dólares en oro representan 2,5*107 de gramos, que corresponden a 25 toneladas.

Es evidente que esto no es posible y que tanto oro no puede caber en una maleta 


5. Magnitudes, Vectores, Sistemas de Coordenadas y Suma de vectores 


Figura 7: Probeta con líquidos
de diferentes densidades.

 5.1 Magnitud escalar
Otras cantidades de la Física y de las ciencias se caracterizan por tener solo magnitud, por ejemplo, la masa (10 kg), longitud (15 m) y temperatura (300 K). A estas cantidades se las denomina magnitudes escalares, para diferenciarlas de las magnitudes vectoriales. Sin embargo, debe recalcarse que aparte de tener unidades tales como kilogramos, metro grados, los escalares no son mas que números reales. Por eso es posible denotarlos con letras comunes. 
Enlace: densidad

5.2 Magnitud vectorial
Hay cantidades en Física y en otras ciencias que para poder ser definidas deben tener magnitud, dirección y sentido, tales como desplazamiento, velocidad, fuerza, aceleración, campo eléctrico. 
Figura 8: Campo eléctrico producido por un
conjunto de cargas puntuales.

 5.3 Vector

Ahora, para describir estas cantidades definimos el concepto de “Vector”, como el segmento que pasa de un punto inicial a otro punto denominado final. Los vectores se denotan en negritas o con letras mayúsculas con una flecha sobre ellas.


5.3.1 Características de un vector.

Un vector, tiene tres características principales:

Módulo: longitud del segmento.
Dirección: orientación de la recta (ángulo).
Sentido: indica cual es el punto de aplicación y el punto final de la recta.

Figura 9: Características de un vector.
5.3.2 Clasificación de vectores

Según los criterios que se utilicen para determinar la igualdad o equipolencia de dos vectores, pueden distinguirse distintos tipos de los mismos:

  • Vectores libres: no están aplicados en ningún punto en particular.
  • Vectores deslizantes: su punto de aplicación puede deslizar a lo largo de su recta de acción.
  • Vectores fijos o ligados: están aplicados en un punto en particular.
  • Vectores concurrentes o angulares: son aquellas cuyas direcciones o líneas de acción pasan por un mismo punto. También se les suele llamar angulares porque forman un ángulo entre ellas.
  • Vectores opuestos: vectores de igual magnitud y dirección, pero sentidos contrarios. En inglés se dice que son de igual magnitud, pero direcciones contrarias, ya que la dirección también indica el sentido.
  • Vectores colineales: los vectores que comparten una misma recta de acción.
  • Vectores paralelos: si sobre un cuerpo rígido actúan dos o más fuerzas cuyas líneas de acción son paralelas.
  • Vectores unitarios: son vectores cuyo módulo es la unidad.
  • Vectores coplanarios: los vectores cuyas rectas de acción son coplanarias (situadas en un mismo plano).



5.3.3 Componentes de vectores

Un vector “V” en dos dimensiones puede separarse en sus dos componentes x e y.



Figura 10: Componentes de un vector en un plano cartesiano.



El vector “V” y sus componentes forman un ángulo.

Figura 11: Ángulo formado entre las componentes de un vector.


Ahora, usando el teorema de Pitágoras podemos calcular la hipotenusa que en este caso representa el módulo del vector “V”.

  |V|2 = Vx2 + Vy2

Para calcular la dirección de un vector debemos apoyarnos en base a las razones trigonométricas.

A continuación, se detalla la tabla de razones trigonométricas en un triángulo rectángulo:



5.3.4 Sistemas de coordenadas

En mecánica se tratan problemas relacionados con la descripción del movimiento de un objeto en el espacio, por lo que se requiere un método para conocer la posición de ese objeto. Para esto se definen los sistemas de coordenadas y marcos de referencia.

Un sistema de coordenadas usado para indicar las posiciones en el espacio consta de:

1. Un punto de referencia fijo O, llamado origen.
2. Un conjunto de ejes o direcciones con una escala apropiada.
3. Instrucciones sobre cómo identificar un punto en el espacio respecto al origen y a los ejes.

5.3.4.0 Sistema de Coordenadas Geográficas


Debemos definir la distribución de los puntos cardinales.
Puntos cardinales
N = Norte
S = Sur
E = Este
O = Oeste



¿Cuál es la diferencia entre latitud y longitud?

Latitud
La latitud, proporciona la localización de un lugar, en dirección Norte o Sur desde el ecuador y se expresa en medidas angulares que varían desde los 0 º

Longitud
La longitud, proporciona la localización de un lugar, en dirección Este u Oeste desde el meridiano de referencia 0 º, o meridiano de Greenwich.


El más frecuente, conocido y casi obligado sistema de coordenadas empleado en los mapas es el llamado sistema geográfico o curvilíneo a base de latitudes y longitudes geográficas. El sistema, como tal fue concebido inicialmente en la Grecia antigua y subsiste sin alteraciones hasta nuestros días. El sistema es curvilíneo debido a que los círculos máximos que lo definen son líneas curvas.

Actividad: Estimar la longitud y latitud de un punto en el globo terrestre.

Latitud y Longitud

Actividad: Coloca correctamente las coordenadas de las siguientes ciudades.

 Coordenadas en el globo terrestre


5.3.4.1 Sistema de Coordenadas Rectangulares o Cartesianas

Uno de los sistemas más usados suele ser, el sistema de coordenadas rectangulares. En este sistema un punto cualquiera se define con tres coordenadas identificadas por (x,y,z),  con valores positivos en los ejes hacia la derecha, hacia arriba y saliendo del plano respectivamente.  

El espacio en el que normalmente vivimos de denomina espacio tridimensional y para indicarlo usamos el símbolo 3D. En ocasiones solo basta con dos o una coordenada para fijar la posición de un objeto, estos se denominan espacio bidimensional (2D) y espacio unidimensional (1D).


Figura 12: Coordenadas rectangulares en un espacio tridimensional (3D)


En el sistema rectangular para un plano bidimensional existen dos ejes, el eje horizontal (x) que se denomina abscisa y el eje vertical (y) que se denomina ordenada. Para representar un punto cualquiera en el plano se denota de la siguiente manera: P (x,y).

Actividad: Ubicar los siguientes puntos desde el siguiente software matemático Geo-Gebra.

Geo-Gebra: Sistema rectangular


Ejemplos:
1. Ubicar los siguientes puntos en el plano cartesiano:
A (-5,3) – B (6,5) – C (4,5,-3,5) – D (0,0)



 2. Calcular la distancia del punto A (1,-2) al punto B (3,-2)

Para calcular la distancia entre dos puntos se aplica la siguiente fórmula: 



3. Calcular el área de un triángulo equilátero, si dos de sus vértices son los puntos P (5,-2) y R (5,2)

En primer lugar, debemos calcular el lado del triángulo usando la fórmula de distancia entre dos puntos.


4. Hallar la pendiente de una recta y el ángulo que pasa por los puntos: A (2,4) y B (6,8)

Para calcular la pendiente entre dos puntos se usa la siguiente fórmula: 

Nota: 
Cuando la pendiente es igual a cero (m = 0), es paralela al eje x.
Cuando la pendiente es indefinida (m = ∞), es paralela al eje y.


Enlace: Simulador PhET - Pendiente

Video: Vector Unitario




 5.3.4.2. Sistema de Coordenadas Polares

En este sistema de coordenadas un punto cualquiera se define como (r, θ), donde r es la distancia desde el origen hasta el punto (x,y) generalmente se llama radio, y θ el ángulo entre el eje x y r, por convección, se considera positivo cuando va en sentido anti horario desde el eje x hacia r.

La relación entre las coordenadas polares y rectangulares o cartesianas es:

x = r (cos θ)      
y = r (sen θ)
r2 =x2 + y2
tan θ = y/x, para un espacio bidimensional

Figura 13: Coordenadas polares de un vector.

Ejemplos:

1. Exprese el siguiente punto en coordenadas cartesianas: P (5, 30º)

La relación para transformar coordenadas polares a cartesianas es:
x = r (cos θ) = 5 (cos 30º) = 4,33      
y = r (sen θ) = 5 (sen 30º) = 2,50
Por lo tanto, el punto en coordenadas cartesianas será: P (4,33; 2,50)


2. Hallar la ecuación polar del lugar geométrico cuya ecuación rectangular es:
x2 + y2 - 4x - 2y + 1 = 0

Podemos reemplazar x2 + y2 por r2, x por r cos θ, y por r sen θ. Por lo tanto, la ecuación polar es:

r2 – 4 r cos θ – 2 r sen θ + 1 = 0


 3. Hallar la ecuación rectangular del lugar geométrico cuya ecuación polar es: r (1 - cos θ) = 2 


Video: Coordenadas polares 




5.3.4.3 Sistemas de Coordenadas Cilíndricas

 El sistema de coordenadas cilíndricas, es un sistema de coordenadas que extiende al sistema de coordenadas polares añadiendo una tercera coordenada que mide la altura de un punto sobre el plano, de la misma forma que el sistema de coordenadas cartesianas se extiende a tres dimensiones. La tercera coordenada se suele representar por h, haciendo que la notación de dichas coordenadas sea (r, θ, h).

 Las coordenadas cilíndricas pueden convertirse en coordenadas cartesianas de la siguiente manera: 

x = r (cos θ)      
y = r (sen θ)
z = h

Figura 14: Coordenadas cilíndricas de un vector.
Ejemplo:
1. Determine las coordenadas cilíndricas de los puntos cuyas coordenadas rectangulares son:
A (3, -2, 1)
B (-7, 10, -6)







5.4 Suma de vectores.

La suma de vectores es bien definida si ambos vectores pertenecen al mismo espacio vectorial, en física para que dos vectores puedan ser sumados deben estar aplicados en el mismo punto.

 5.4.1 Método del Paralelogramo
Figura 15: Suma de dos vectores por el método del paralelogramo.

Este método permite sumar vectores de dos en dos. Consiste en disponer gráficamente los dos vectores de manera que los orígenes de ambos coincidan en un punto, trazando rectas paralelas a cada uno de los vectores, en el extremo del otro y de igual longitud, formando así un paralelogramo. El vector resultante de la suma es la diagonal de dicho paralelogramo que parte del origen común de ambos vectores.








5.4.2 Método del Polígono
Figura 16: Suma de dos vectores por el método del polígono.

Consiste en disponer gráficamente un vector a continuación de otro, ordenadamente: el origen de cada uno de los vectores coincidirá con el extremo del siguiente. El vector resultante es aquel cuyo origen coincide con el del primer vector y termina en le extremo del ultimo.



Enlace: Simulador PhET - Suma de vectores

5.4.3 Método analítico para suma y resta de vectores

Dado dos vectores libres:

A = (Ax) i + (Ay) j + (Az) k
B = (Bx) i + (By) j + (Bz) k

El resultado de la suma o diferencia de vectores será:

A ± B = (Axi + Ayj + Azk) ± (Bxi + Byj + Bzk)

Ordenando por componentes, tenemos:

A ± B = (Ax ± Bx) i + (Ay ± By) j + (Az ± Bz) k



5.4.4 Ley del Coseno

Para sumar vectores de manera analítica, se necesita que estos se encuentren en notación cartesiana o de vectores unitarios.
La ley del coseno nos permite sumar analíticamente los vectores si están en representación polar y evitarnos el cambio de notación.

Sean los vectores A y B los mostrados en la figura, encuentre A + B 
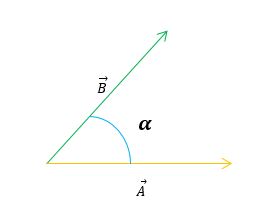Figura 17: Representación de dos vectores formando un ángulo α 


Si realizamos el método gráfico de suma por paralelogramo, podremos observar el vector resultado R y haciendo las proyecciones del vector B y colocamos en función de la magnitud de B y la razón trigonométrica específica para el ángulo α.


Figura 18: Método del paralelogramo


Para el triángulo formado por los puntos XYZ se puede notar que:
•     |R| es la hipotenusa.
•     |B|sen α es el cateto opuesto;  |B|cos α es el cateto adyacente.
Por tanto, estableceremos un Teorema de Pitágoras para hallar la magnitud |B| y el ángulo θR respectivo.

Figura 19: Aplicación del teorema de Pitágoras



Por obvias razones, el ángulo θR es:


5.4.5 Ley del Seno

Usando el mismo gráfico para deducir la ley del coseno, trazamos una bisectriz en el polígono inferior.

Figura 20: Método Paralelogramo y deducción de la Ley del Seno.





6. Producto de vectores.


Hemos visto cómo la suma de vectores es consecuencia natural de combinar desplazamientos, y sumaremos muchas otras cantidades vectoriales posteriormente. También podemos expresar muchas relaciones físicas de forma concisa usando producto de vectores. Los vectores no son números ordinarios, así que no podemos aplicarles directamente la multiplicación ordinaria. Definiremos dos tipos diferentes de productos de vectores. El primero, llamado producto escalar, produce un resultado escalar. El segundo, el producto vectorial, produce otro vector.

6.1 Producto escalar.
Figura 21: Proyección del vector A hacia B.
El producto escalar de dos vectores A y B se denota con A·B. Por esta notación, el producto escalar también se denomina producto punto. Aun cuando A y B sean vectores, la cantidad A·B es un escalar.
El producto escalar de dos vectores en un espacio euclidiano se define como el producto de sus módulos por el coseno del ángulo {\displaystyle \theta }θ que forman.


A · B = |A| |B| cos θ
Donde:
|A| = magnitud del vector A
|B| = magnitud del vector B
θ = ángulo entre los dos vectores


6.1.1 Ángulo entre dos vectores.

La expresión del producto escalar nos permite calcular el coseno del ángulo que existe entre dos vectores.

6.1.2 Vectores ortogonales.
Dos vectores son ortogonales o perpendiculares cunado el ángulo que forman entres los dos es un ángulo recto (90º).
A · B = 0                 A ┴ B

6.1.3 Vectores paralelos.
Dos vectores son paralelos si el ángulo que forman entre ambos es de cero grados (0º) o de ciento ochenta grados (180º).
A · B = |A| |B|

6.1.4 Cálculo de producto escalar usando sus componentes.
Podemos calcular el producto escalar A · B directamente si conocemos las componentes x, y, z, de los vectores A y B.
En primer lugar, debemos saber los productos escalares de los vectores unitarios (î, ĵ, k).

î · î  cos θ = (1) (1) cos (0º) = 1
ĵ · ĵ  cos θ = (1) (1) cos (0º) = 1
k · k cos θ= (1) (1) cos (0º) = 1

î · ĵ cos θ  = (1) (1) cos (90º) = 0
î · k cos θ = (1) (1) cos (90º) = 0
ĵ · k cos θ = (1) (1) cos (90º) = 0

Ahora, expresamos los vectores A y B en términos de sus componentes y usamos los productos escalares de los vectores unitarios.

A · B = (Ax î + Ay ĵ + Az k) · (Bx î + By ĵ + Bz k)
A · B = Ax Bx + Ay By + Az Bz

Por lo tanto, el producto escalar entre dos vectores es la suma de los productos de sus respectivas componentes.

 Video: Proyección vectorial.


Ejemplos:
1. En la siguiente figura se muestran dos vectores. Obtenga el producto escalar A · B si las magnitudes de los vectores son: 
A = 4,00 y B = 5,00

Figura 22: Dos vectores en dos dimensiones.
Hay dos formas de calcular el producto escalar.
  • La primera consiste en usar las magnitudes de los vectores y el ángulo que forman entre ellos.
El ángulo entre los dos vectores es:
ϕ = 130,0 º – 53,0 º = 77º

A · B = |A| |B| cos θ
A · B = (4,00) (5,00) cos 77º
A · B = 4,5


  • La segunda consiste en usar las componentes de ambos vectores.
Ax = (4,00) cos 53,0 º = 2,41                    Bx = (5,00) cos 130,0 º = - 3,21
Ay = (4,00) sen 53,0 º = 3,19                    By = (5,00) sen 130,0 º = 3,83
Az = 0                                                        Bz = 0

 Las componentes z son cero, porque ambos vectores están en el plano xy.
A · B = Ax Bx + Ay By + Az Bz
A · B = (2,41) (-3,21) + (3,19) (3,83) + (0) (0)
A · B = 4,5


2. Determine el ángulo entre los dos vectores:
A = 2î + 3ĵ + k           y           B = -4î + 2ĵ - k

Figura 23: Dos vectores en tres dimensiones.

Calculamos el módulo de cada vector:
Luego, calculamos el producto punto entre ambos vectores:
A · B = Ax Bx + Ay By + Az Bz
A · B = (2) (-4) + (3) (2) + (1) (-1)
A · B = -3

Usamos la fórmula para calcular el ángulo entre dos vectores: 











Video: Vectores paralelos o perpendiculares.





6.2 Producto vectorial
El producto vectorial entre dos vectores da como resultado un vector, se lee A cruz B, y se define como:
C = A x B
|C| = |A| |B| sen θ

Donde:
|A| = magnitud del vector A
|B| = magnitud del vector B
C = vector perpendicular al plano formado por A y B
θ = ángulo entre los dos vectores

El producto vectorial se calcula resolviendo el siguiente determinante: 


Aplicado a vectores unitarios, se obtiene que:
 î x î = ĵ x ĵ = k x k = 0
 î x ĵ = k    ĵ x k = î   k x î = ĵ

Ejemplo:
1. El vector A tiene una magnitud de 6 unidades y está sobre el eje +x. El vector B tiene una magnitud de 4 unidades y está en el plano xy formando un ángulo de 30 º con el eje +x (ver figura).

Calcule el producto cruz A x B.
Figura 24: Vectores A y B y su producto vectorial C = A x B
Podemos obtener el producto cruz de dos maneras:
  • La primera consiste, en usar la fórmula de producto cruz y luego la regla de la mano derecha:

|A x B| = |A| |B| sen θ
|A x B| = (6) (4) sen 30 º
|A x B| = 12

Por la regla de la mano derecha A x B, tiene la dirección del eje +z, por lo tanto:
A x B = 12 k

  • La segunda manera consiste en usar determinantes:
Debemos calcular las componentes de los dos vectores en coordenadas rectangulares.

 Ax = 6                          Bx = 4 cos 30º = 3,46
Ay = 0                          By = 4 sen 30º = 2,00
Az = 0                          Bz = 0


A x B = î (0*0 – 0*2,00) – ĵ (6*0 – 0*3,46) + k (6*2,00 – 0*3,46)
A x B = 0î - 0ĵ + 12k
A x B = 12 k

Video: Producto escalar y producto vectorial




7. Ejercicios / Problemas











Etiquetas: